Objectives
HL 4.13
Evaluation of least squares regression curves using technology.
Sum of square residuals (SSres) as a measure of fit for a model.
The coefficient of determination (R2). Evaluation of R2 using technology.
Non-linear regression.
Linear Regression
In the standard level unit you have thought about the least square regression line and how to get the equation for the line in your GDC. I have already explained that you can only predict y from x and NOT x from y using this equation.
Two more important points to remember are DO NOT extrapolate and a linear model is only as good as the strength of the correlation.
If you encounter a set of data that shows two obvious linear trends, you can separate the data into two sections and establish a regression line for each section.
The regression line is a linear model and as such, it has predictive powers. It can be used to predict a value not stated within the range of the data set. So, for example, if you were comparing height with weight and you had data points for 1.23m, 1.24m, and 1.29m, the linear model allows you to predict the weight of an individual 1.26m tall.
You may now be asking, but how good is this line at predicting values? It is possible to measure the predictive power of a linear model. For this, we use the coefficient of determination R squared.
The value of the coefficient of determination can be interpreted as a percentage. So, if R squared is 0.83, then you can say that the least square regression line successfully predicted 83% of the variation in the dependent variable.
You will pleased to know that your GDC will calculate the coefficient of determination for you.
Watch Revision Village Coefficient of Determination video.
Now, work through Khans Academy Statistics and Probability Unit 5 Assessing the fit in least-squares regression and Quiz 4.
Complete the five questions on the worksheet below.
Non-Linear Regression
While linear regression helps us model relationships with straight lines, not all relationships in the real world are linear. This is where non-linear regression comes in. Let’s break it down!
Non-linear regression is a method used to model relationships between variables when the data does not follow a straight line. Instead of fitting a linear equation (y=mx+c), non-linear regression fits a curve to the data based on a mathematical model.
Non-linear regression allows you to model complex real-world relationships that cannot be represented by straight lines. From predicting population growth to understanding oscillating patterns in physics, it’s a powerful tool in your mathematical toolkit.
Key Characteristics:
The equation describing the relationship is non-linear in its parameters.
Common forms include quadratic, exponential, logarithmic, power, and sinusoidal models.
Non-linear regression often requires technology (like graphing calculators or software) to perform accurately.
Types of Non-Linear Regression Models
Here are a few common types of models you’ll encounter:
Quadratic Models
Equation:

Example: Modeling the trajectory of a ball thrown in the air.
Recognizing it: Look for a parabolic shape in the data.
Cubic Models
Equation:

Example: Modeling complex growth patterns, such as the spread of a disease that starts slowly, accelerates, and then slows down.
Recognizing it: The scatterplot shows an "S-shaped" curve or multiple changes in direction.
Power Models
Equation:

Example: Modeling relationships like the surface area vs. volume of a growing object or the relationship between speed and stopping distance in physics.
Recognizing it: Data shows a curve that increases or decreases rapidly, but not exponentially. Power models often appear when one quantity grows proportionally to a power of another.
Exponential Models
Equation:

Example: Modeling population growth or radioactive decay.
Recognizing it: Rapid growth or decay in the data.
Logarithmic Models
Equation:
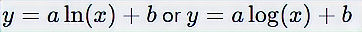
Example: Modeling the diminishing returns in learning curves.
Recognizing it: Data increases quickly at first, then levels off.
Sinusoidal Models
Equation:

Example: Modeling seasonal weather patterns or sound waves.
Recognizing it: Repeated oscillations in the data.
Linearising Non-Linear Data Mean?
Linearisation is a method used to transform non-linear data into a straight line by applying a mathematical operation (like taking the logarithm or reciprocal of one or both variables). Once transformed, linear regression techniques can be used to analyse the relationship between variables.
Why Linearise Data?
Simplifies Analysis: It’s easier to interpret and model a straight-line relationship than a curved one.
Allows Use of Linear Regression: Many statistical tools and calculators are optimised for linear regression.
Reveals Hidden Relationships: Linearisation can highlight patterns that are less obvious in the raw data.
Logarithms are a key tool in this process. Let’s explore how logarithmic transformations work and how they help.
Why logarithms help:
They compress data, reducing large ranges of values to manageable scales.
They linearize certain relationships, allowing us to analyze them with straight-line techniques.
They reveal proportional relationships hidden in non-linear data.
How to do this (it will be in the video below as well)
Input the data in your GDC, then apply a logarithm to the data points.
Determine which expression did the best job.
Find the least squares regression line.
Use knowledge of exponents and logarithms to find the
non-linear model.
Watch Revision Villages Non-Linear Regression video.
Understanding Logarithmic Axes
As an IB Mathematics HL student, you’re likely to encounter a variety of graph types in your studies. One of the more unique representations is the logarithmic scale. While it may seem daunting at first, mastering how to interpret logarithmic axes can be incredibly beneficial, especially in fields like science and engineering where data can span several orders of magnitude.
What is a Logarithmic Scale?
A logarithmic scale is a nonlinear scale used to represent data that covers a large range of values. Instead of increasing linearly, each unit on a logarithmic axis, often called a log scale, corresponds to an exponent. For instance, on a base-10 logarithmic scale:
1 on the scale represents

2 represents

3 represents

4 represents

This means each step on the axis represents a tenfold increase (in the case of base-10 logarithm) rather than a simple addition of units. This is invaluable when graphing information such as population growth, earthquake magnitudes, or sound intensity, where values can vary dramatically.
Advantages of Using Logarithmic Axes
1. Simplifying Large Data Ranges: Logarithmic scales condense large
variations in data, making it easier to visualise and analyse relationships.
2. Identifying Patterns: A linear relationship can often appear as a straight
line on a log scale, enabling easier interpretation of exponential growth or
decay.
3. Highlighting Percentage Changes: Since log scales depict multiplicative
factors, they illustrate relative changes more effectively than linear scales.
Interpreting Logarithmic Axes
1. Understand the Scale: When you first look at a log scale, take a moment to
familiarise yourself with the values represented. Ensure you know whether
it’s a base-10 log or a natural log (base e). This is crucial for accurately
interpreting the data.
2. Calculate Values: If you need the actual values represented on a log scale, use the inverse function of the logarithm. For example, if you see a point
plotted at 3 on a base-10 logarithmic axis, it represents 1000.
3. Analyse Relationships: Use the properties of logarithms to infer
relationships. For instance, a straight line on a log-log plot (both axes
logarithmic) suggests a power law relationship. Similarly, a straight line on a
semilogarithmic plot (one axis linear, the other logarithmic) indicates
exponential growth.
4. Compare Data Sets: Logarithmic scales are particularly useful when
comparing multiple datasets. Since each dataset can be stretched or
compressed without losing its foundational relationships, it allows you to
make visual comparisons even when the scales differ.
Watch OSC Lineraisation video.
On your GDC watch IBvodcasting Linerization video.
Practice
Complete the worksheet below using your GDC. There is an answer sheet provided to help you determine whether you understand the concepts.

Comments